Bayesian Optimization¶

Pure Python implementation of bayesian global optimization with gaussian processes.

This is a constrained global optimization package built upon bayesian inference and gaussian processes, that attempts to find the maximum value of an unknown function in as few iterations as possible. This technique is particularly suited for optimization of high cost functions and situations where the balance between exploration and exploitation is important.

Installation¶

pip (via PyPI)¶

$ pip install bayesian-optimization

Conda (via conda-forge)¶

$ conda install -c conda-forge bayesian-optimization

How does it work?¶

Bayesian optimization works by constructing a posterior distribution of functions (gaussian process) that best describes the function you want to optimize. As the number of observations grows, the posterior distribution improves, and the algorithm becomes more certain of which regions in parameter space are worth exploring and which are not, as seen in the picture below.

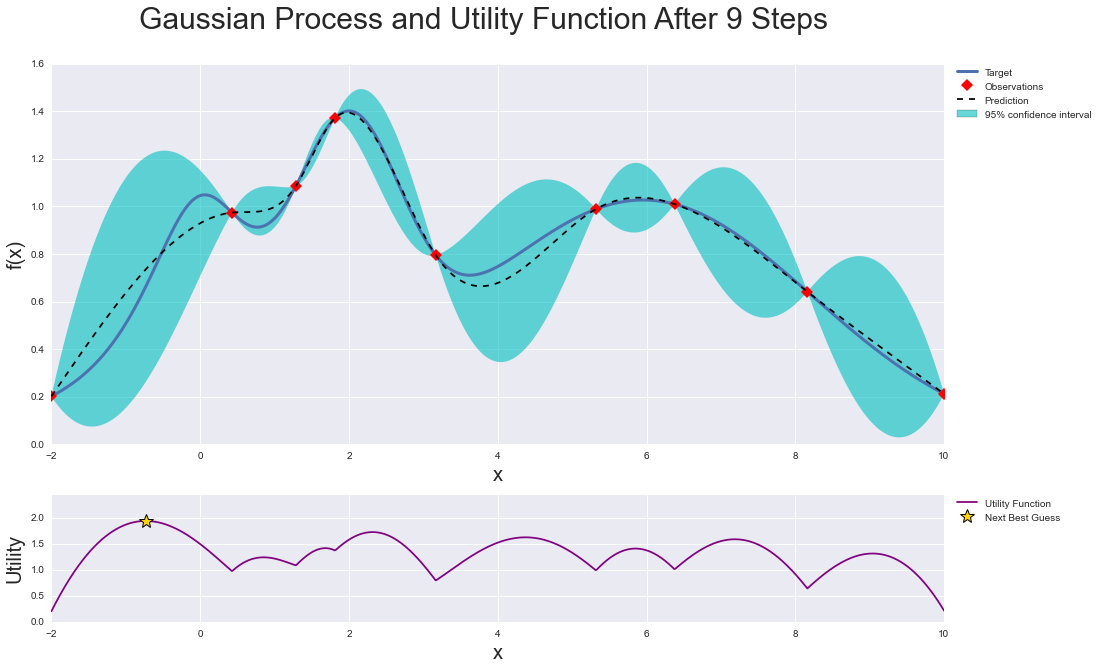
As you iterate over and over, the algorithm balances its needs of exploration and exploitation taking into account what it knows about the target function. At each step a Gaussian Process is fitted to the known samples (points previously explored), and the posterior distribution, combined with a exploration strategy (such as UCB (Upper Confidence Bound), or EI (Expected Improvement)), are used to determine the next point that should be explored (see the gif below).

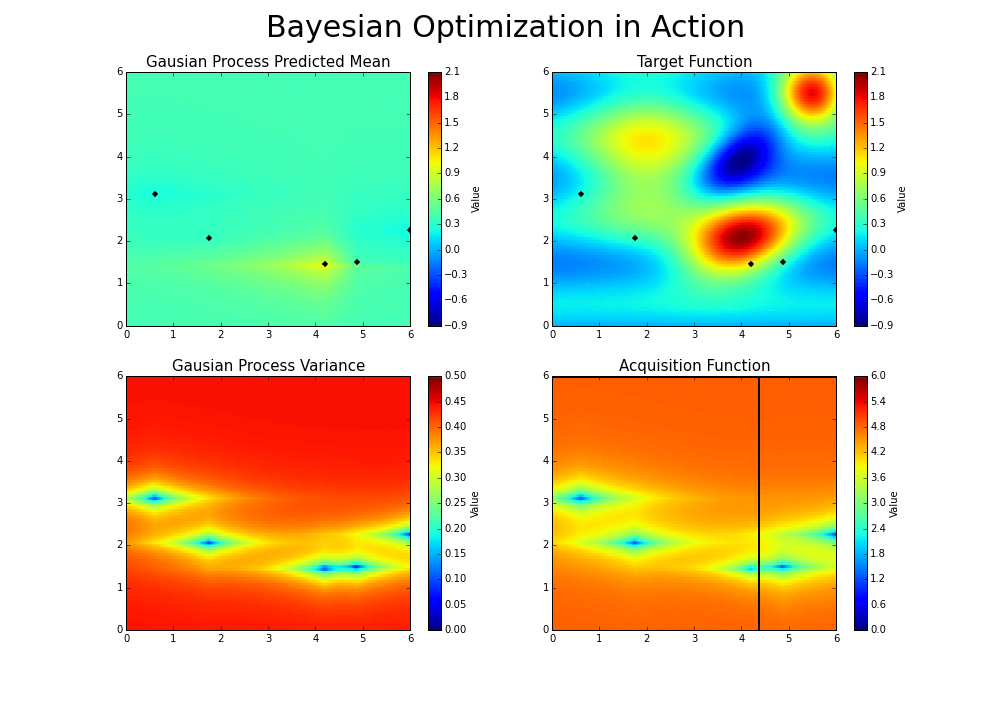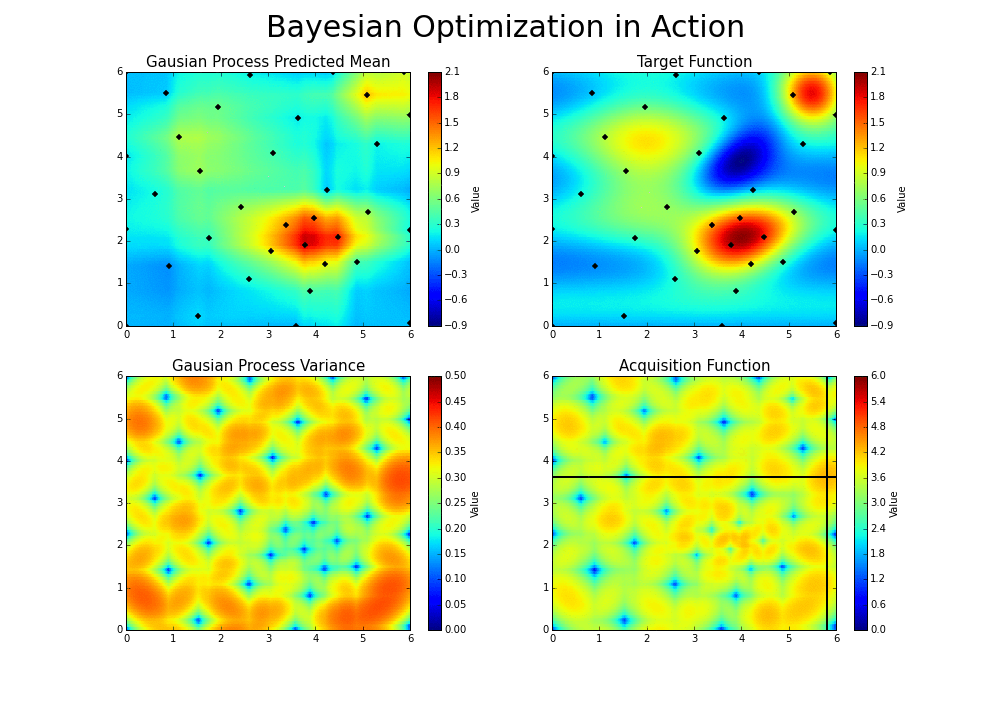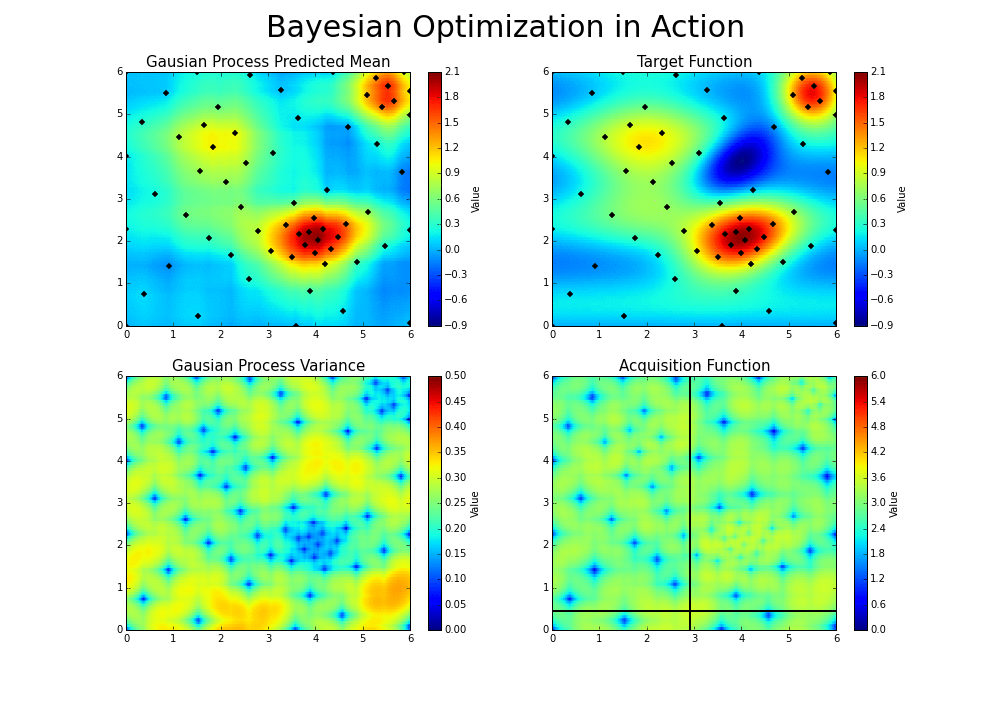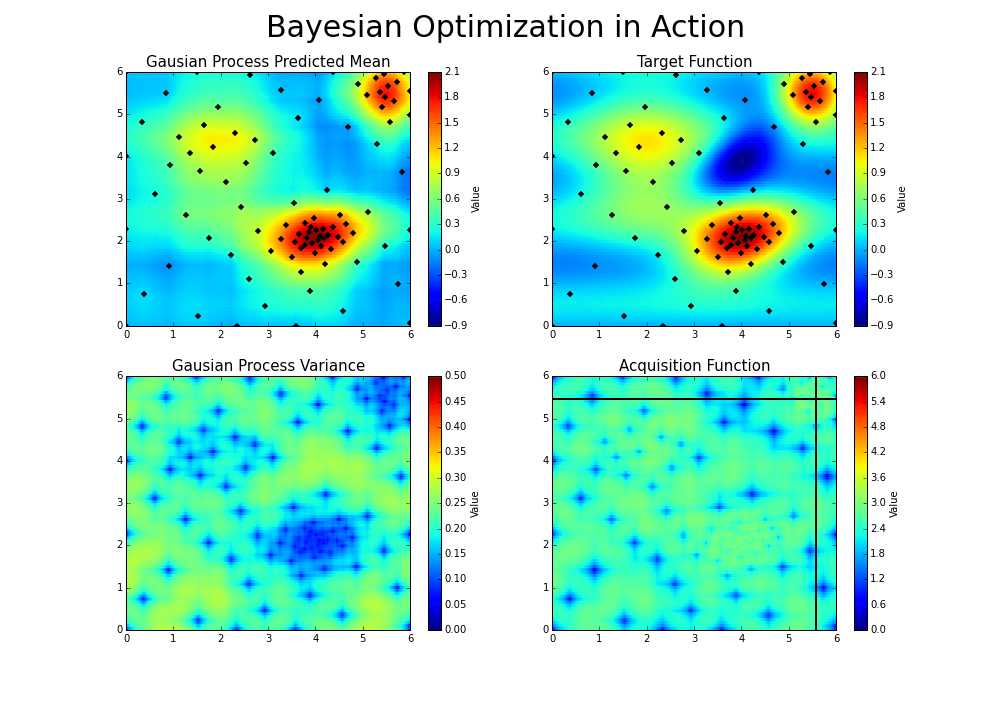
This process is designed to minimize the number of steps required to find a combination of parameters that are close to the optimal combination. To do so, this method uses a proxy optimization problem (finding the maximum of the acquisition function) that, albeit still a hard problem, is cheaper (in the computational sense) and common tools can be employed. Therefore Bayesian Optimization is most adequate for situations where sampling the function to be optimized is a very expensive endeavor. See the references for a proper discussion of this method.

This project is under active development, if you find a bug, or anything that needs correction, please let us know by filing an issue on GitHub .

Quick Index¶

See below for a quick tour over the basics of the Bayesian Optimization package. More detailed information, other advanced features, and tips on usage/implementation can be found in the examples section. We suggest that you:

• Follow the basic tour notebook to learn how to use the package’s most important features.

• Take a look at the advanced tour notebook to learn how to make the package more flexible, how to deal with categorical parameters, how to use observers, and more.

• Check out this notebook with a step by step visualization of how this method works.

• To understand how to use bayesian optimization when additional constraints are present, see the constrained optimization notebook.

• Explore the domain reduction notebook to learn more about how search can be sped up by dynamically changing parameters’ bounds.

• Explore this notebook exemplifying the balance between exploration and exploitation and how to control it.

• Go over this script for examples of how to tune parameters of Machine Learning models using cross validation and bayesian optimization.

• Finally, take a look at this script for ideas on how to implement bayesian optimization in a distributed fashion using this package.

Citation¶

If you used this package in your research, please cite it:

@Misc{,
    author={Fernando Nogueira},
    title={{Bayesian Optimization}: Open source constrained global optimization tool for {Python}},
    year={2014--},
    url="https://github.com/bayesian-optimization/BayesianOptimization"
}

If you used any of the advanced functionalities, please additionally cite the corresponding publication:

For the SequentialDomainTransformer:

@article{
    author={Stander, Nielen and Craig, Kenneth},
    year={2002},
    month={06},
    pages={},
    title={On the robustness of a simple domain reduction scheme for simulation-based optimization},
    volume={19},
    journal={International Journal for Computer-Aided Engineering and Software (Eng. Comput.)},
    doi={10.1108/02644400210430190}
}

For constrained optimization:

@inproceedings{gardner2014bayesian,
    title={Bayesian optimization with inequality constraints.},
    author={Gardner, Jacob R and Kusner, Matt J and Xu, Zhixiang Eddie and Weinberger, Kilian Q and Cunningham, John P},
    booktitle={ICML},
    volume={2014},
    pages={937--945},
    year={2014}
}